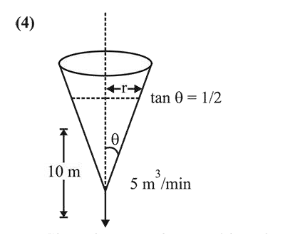
A water tank has the shape of an inverted right circular cone, whose semi-vertical angle is $\tan ^{-1}\left(\frac{1}{2}\right)$. Water is
poured into it at a constant rate of 5 cubic meter per minute. Then the rate (in $\mathrm{m} / \mathrm{min}$.), at which the level of water is rising at the instant when the depth of water in the tank is $10 \mathrm{~m}$; is:
Correct Option:
 '
'
Given that water is poured into the tank at a constant rate of $5 \mathrm{~m}^{3} /$ minute.'
$\therefore \frac{d v}{d t}=5 \mathrm{~m}^{3} / \mathrm{min}$'
Volume of the tank is,
$V=\frac{1}{3} \pi r^{2} h$ ..............(1)
where $r$ is radius and $h$ is height at any time.
By the diagram,
$\tan \theta=\frac{r}{h}=\frac{1}{2}$
$\Rightarrow h=2 r \Rightarrow \frac{d h}{d t}=\frac{2 d r}{d t}$ .........(2)
Differentiate eq. (i) w.r.t. ' $t$ ', we get
$\frac{d V}{d t}=\frac{1}{3}\left(\pi 2 r \frac{d r}{d t} h+\pi r^{2} \frac{d h}{d t}\right)$
Putting $h=10, r=5$ and $\frac{d V}{d t}=5$ in the above equation.
$5=\frac{75 \pi}{3} \frac{d h}{d t} \Rightarrow \frac{d h}{d t}=\frac{1}{5 \pi} \mathrm{m} / \mathrm{min}$
