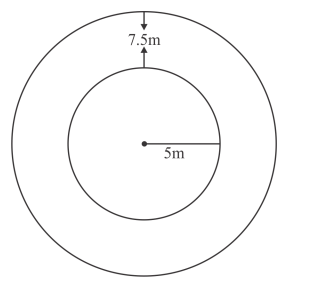
A well with 10 m inside diameter is dug 8.4 m deep.

Radius of well

Depth of well h = 8.4 m

Clearly,

Volume of earth dugout

$=\pi(5)^{2} \times 8.4$

$=\pi \times 25 \times 8.4$

$=\frac{22 \times 25 \times 8.4}{7} \mathrm{~m}^{3}$

Let h' be the height of embankment

Clearly,

Embankment forms a cylindrical shell whose inner and outer radius are 5 m and 12.5 m respectively.

 Volume of the embankment

$=\pi\left\{(12.5)^{2}-(5)^{2}\right\} \times h^{\prime}$

$=\pi \times 17.5 \times 7.5 \times h^{\prime} \mathrm{m}^{3}$

But, volume of earth dugout = volume of the embankment

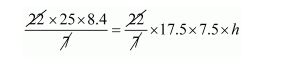
$h=\frac{25 \times 8.4}{17.5 \times 7.5}$

$h^{\prime}=1.6 \mathrm{~m}$