A wheel is rotaing freely with an angular speed $\omega$ on a shaft. The moment of inertia of the wheel is I and the moment of inertia of the shaft is negligible. Another wheel of momet of inertia 3I initially at rest is suddenly coupled to the same shaft. The resultant fractional loss in the kinetic energy of the system is :
Correct Option: , 3
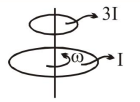
By anglar momentum conservation
$\omega I+3 I \times 0=4 I \omega^{\prime} \Rightarrow \omega^{\prime}=\frac{\omega}{4}$
$(\mathrm{KE})_{\mathrm{i}}=\frac{1}{2} \mathrm{I} \omega^{2}$
$(\mathrm{KE})_{\mathrm{f}}=\frac{1}{2} \times(4 \mathrm{I}) \times\left(\frac{\omega}{4}\right)^{2}=\frac{\mathrm{I} \omega^{2}}{8}$
$\Delta \mathrm{KE}=\frac{3}{8} \mathrm{I} \omega^{2}$
fractional loss $=\frac{\Delta \mathrm{KE}}{\mathrm{KE}_{1}}=\frac{\frac{3}{8} \mathrm{I} \omega^{2}}{\frac{1}{2} \mathrm{I} \omega^{2}}=\frac{3}{4}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
