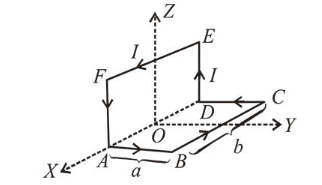
A wire carrying current $I$ is bent in the shape $A B C D E F A$ as shown, where rectangle $A B C D A$ and $A D E F A$ are perpendicular to each other. If the sides of the rectangles are of lengths $a$ and $b$, then the magnitude and direction of magnetic moment of the loop $A B C D E F A$ is :
Correct Option: 1
(1) Magnetic moment of loop $A B C D$,
$M_{1}=$ area of loop $\times$ current
$\vec{M}_{1}=(a b I)(\hat{j})$ (Here, $a b=$ area of rectangle)
Magnetic moment of loop $D E F A$,
$\vec{M}_{2}=(a b I)(\hat{i})$c
Net magnetic moment,
$\vec{M}=\vec{M}_{1}+\vec{M}_{2} \Rightarrow \vec{M}=a b I(\hat{i}+\hat{j})$
$\Rightarrow|\vec{M}|=\sqrt{2} a b I\left(\frac{\hat{j}}{\sqrt{2}}+\frac{\hat{k}}{\sqrt{2}}\right)$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
