A wire of length $36 \mathrm{~m}$ is cut into two pieces, one of the pieces is bent to form a square and the other is bent to form a circle. If the sum of the areas of the two figures is minimum, and the circumference of the circle is $\mathrm{k}$ (meter), then $\left(\frac{4}{\pi}+1\right) \mathrm{k}$ is equal to _______.
Let $x+y=36$
$x$ is perimeter of square and $y$ is perimeter of circle side of square $=\mathrm{x} / 4$
radius of circle $=\frac{\mathrm{y}}{2 \pi}$
Sum Areas $=\left(\frac{\mathrm{x}}{4}\right)^{2}+\pi\left(\frac{\mathrm{y}}{2 \pi}\right)^{2}$
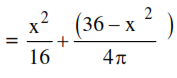
For min Area :
$x=\frac{144}{\pi+4}$
$\Rightarrow$ Radius $=\mathrm{y}=36-\frac{144}{\pi+4}$
$\Rightarrow \mathrm{k}=\frac{36 \pi}{\pi+4}$
$\left(\frac{4}{\pi}+1\right) \mathrm{k}=36$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
