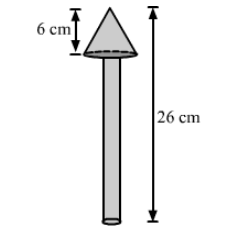
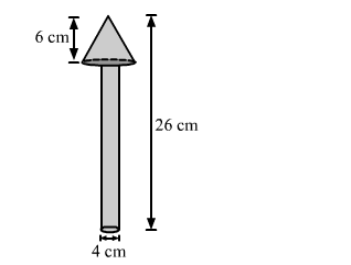
A wooden toy is in the shape of a cone mounted on a cylinder, as shown in the figure.

We have,

the base radius of the conical part, $r=\frac{5}{2}=2.5 \mathrm{~cm}$,

the base radius of the cylindrical part, $R=\frac{4}{2}=2 \mathrm{~cm}$,

the total height of the toy $=26 \mathrm{~cm}$,

the height of the conical part, $h=6 \mathrm{~cm}$

Also, the height of the cylindrical part, $H=26-6=20 \mathrm{~cm}$

And, the slant height of the conical part, $l=\sqrt{r^{2}+h^{2}}=\sqrt{2.5^{2}+6^{2}}=\sqrt{6.25+36}=\sqrt{42.25}=6.5 \mathrm{~cm}$

Now,

The area to be painted by red colour $=$ CSA of cone $+$ Area of base of conical part $-$ Area of base of cylindrical part

$=\pi r l+\pi r^{2}-\pi R^{2}$

$=\frac{22}{7} \times 2.5 \times 6.5+\frac{22}{7} \times 2.5 \times 2.5-\frac{22}{7} \times 2 \times 2$

$=\frac{22}{7} \times 16.25+\frac{22}{7} \times 6.25-\frac{22}{7} \times 4$

$=\frac{22}{7} \times(16.25+6.25-4)$

$=\frac{22}{7} \times 18.5$

$\approx 58.14 \mathrm{~cm}^{2}$

Also,

The area to be painted by white colour $=$ CSA of cylinder $+$ Area of base of cylinder

$=2 \pi R H+\pi R^{2}$

$=\pi R(2 H+R)$

$=\frac{22}{7} \times 2 \times(2 \times 20+2)$

$=\frac{22}{7} \times 2 \times 42$

$=264 \mathrm{~cm}^{2}$