AB and AC are two chords of a circle of radius

Given In a circle of radius $r$, there are two chords $A B$ and $A C$ such that $A B=2 A C$. Also, the distance of $A B$ and $A C$ from the centre are $p$ and $q$, respectively.

To prove $4 q^{2}=p^{2}+3 r^{2}$

Proof Let $A C=a$, then $A B=2 a$

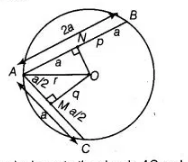
From centre $O$, perpendicular is drawn to the chords $A C$ and $A B$ at $M$ and $N$, respectively.

$\therefore$ $A M=M C=\frac{a}{2}$

$A N=N B=a$

In $\Delta O A M$ $A O^{2}=A M^{2}+M O^{2}$ [by Pythagoras theorem]

$\Rightarrow$ $A O^{2}=\left(\frac{a}{2}\right)^{2}+q^{2}$  $\ldots(1)$

In $\triangle O A N$, use Pythagoras theorem,

$A O^{2}=(A N)^{2}+(N O)^{2}$

$\Rightarrow \quad A O^{2}=(a)^{2}+p^{2} \quad \ldots$ (ii)

From Eqs. (i) and (ii),

$\left(\frac{a}{2}\right)^{2}+q^{2}=a^{2}+p^{2}$

$\Rightarrow \quad \frac{a^{2}}{4}+q^{2}=a^{2}+p^{2}$

$\Rightarrow \quad a^{2}+4 q^{2}=4 a^{2}+4 p^{2} \quad$ [multiplying both sides by 4]

$\Rightarrow \quad 4 q^{2}=3 a^{2}+4 p^{2}$

$\Rightarrow \quad 4 q^{2}=p^{2}+3\left(a^{2}+p^{2}\right)$

$\Rightarrow \quad 4 q^{2}=p^{2}+3 r^{2} \quad\left[\right.$ In right angled $\left.\Delta O A N, r^{2}=a^{2}+p^{2}\right]$

Hence proved.