AB is a diameter of a circle and AC is its chord such that ∠BAC – 30°. If the tangent at C intersects AB extended at D, then BC = BD.
True
To Prove, BC = BD
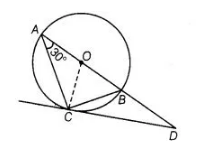
Join $B C$ and $O C$.
Given, $\angle B A C=30^{\circ}$
$\Rightarrow$ $\angle B C D=30^{\circ}$
[angle between tangent and chord is equal to angle made by chord in the alternate segment]
$\therefore$$\angle A C D=\angle A C O+\angle O C D=30^{\circ}+90^{\circ}=120^{\circ}$
$\left[\because O C \perp C D\right.$ and $O A=O C=$ radius $\left.\Rightarrow \angle O A C=\angle O C A=30^{\circ}\right]$
$\ln \triangle A C D \quad \angle C A D+\angle A C D+\angle A D C=180^{\circ}$
[since, sum of all interior angles of a triangle is $180^{\circ}$ ]
$\Rightarrow \quad 30^{\circ}+120^{\circ}+\angle A D C=180^{\circ}$
$\Rightarrow \quad \angle A D C=180^{\circ}-\left(30^{\circ}+120^{\circ}\right)=30^{\circ}$
Now in $\triangle B C D \quad \angle B C D=\angle B D C=30^{\circ}$
$\Rightarrow \quad B C=B D$
[since, sides opposite to equal angles are equal]