AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from

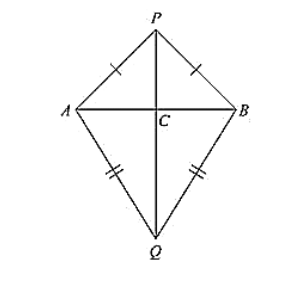
Consider the figure.

We have

AB is a line segment and P, Q are points on opposite sides of AB such that

AP = BP    ... (i)

AQ = BQ     ... (ii)

We have to prove that PQ is perpendicular bisector of AB.

Now consider ΔPAQ and ΔPBQ,

We have

AP = BP                    [From (i)]

AQ = BQ                   [From (ii)]

And PQ - PQ             [Common site]

Δ PAQ ≃ Δ PBQ  ... (iii)  [From SAS congruence]

Now, we can observe that APB and ABQ are isosceles triangles. [From (i) and (ii)]

∠ PAB = ∠ ABQ and ∠ QAB = ∠ QBA

Now consider Δ PAC and Δ PBC

C is the point of intersection of AB and PQ

PA = PB                       [From (i)]

∠ APC = ∠ BPC           [From (ii)]

PC = PC                        [common side]

So, from SAS congruency of triangle ΔPAC ≅ ΔPBC

AC = CB and ∠PCA = ∠PBC ... (iv)   [Corresponding parts of congruent triangles are equal]                           

And also, ACB is line segment

∠ACP + ∠ BCP = 180°

∠ACP = ∠PCB

∠ACP = ∠PCB = 90°<

We have AC = CB ⟹ C is the midpoint of AB

From (iv) and (v)

We can conclude that PC is the perpendicular bisector of AB

Since C is a point on the line PQ, we can say that PQ is the perpendicular bisector of AB.