ABC and BDE are two equilateral triangles

True

Given, $\triangle A B C$ and $\triangle B D E$ are two equilateral triangles.

$\therefore$ Area of an equilateral $\triangle A B C=\frac{\sqrt{3}}{4} \times(\text { Side })^{2}=\frac{\sqrt{3}}{4}(B C)^{2}$ $\ldots(1)$

$[\because$ in equilateral $\triangle A B C, A B=B C=A C]$

Also, given $D$ is the mid-point of $B C$.

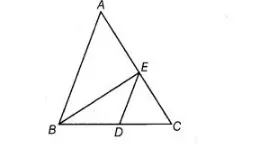
$\therefore$ $B D=D C=\frac{1}{2} B C$ ...(ii)

Now, area of an equilateral $\triangle B D E=\frac{\sqrt{3}}{4} \times(\text { Side })^{2}$ 

$=\frac{\sqrt{3}}{4} \times(B D)^{2}$ $[\because$ in equilateral $\triangle B D E, B D=D E=B E]$

$=\frac{\sqrt{3}}{4} \times\left(\frac{1}{2} B C\right)^{2}$ [from Eq. (ii)]

$=\frac{\sqrt{3}}{4} \times \frac{1}{4} B C^{2}=\frac{1}{4}\left(\frac{\sqrt{3}}{4} B C^{2}\right)$

$\therefore$ Area of $\triangle B D E=\frac{1}{4}$ Area of $\triangle A B C$