∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is

Given: ΔABC and ΔBDE are two equilateral triangles such that D is the midpoint of BC.

To find: Ratio of areas of ΔABC and ΔBDE.

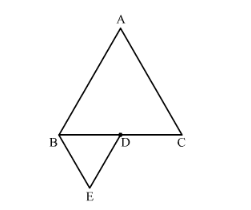
ΔABC and ΔBDE are equilateral triangles; hence they are similar triangles.

Since D is the midpoint of BC, BD = DC.

We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.

$\frac{\operatorname{ar}(\Delta \mathrm{ABC})}{\operatorname{ar}(\Delta \mathrm{BDE})}=\left(\frac{\mathrm{BC}}{\mathrm{BD}}\right)^{2}$

$\frac{\operatorname{ar}(\Delta \mathrm{ABC})}{\operatorname{ar}(\Delta \mathrm{BDE})}=\left(\frac{\mathrm{BD}+\mathrm{DC}}{\mathrm{BD}}\right)^{2}[\mathrm{D}$ is the midpoint of $\mathrm{BC}]$

$\frac{\operatorname{ar}(\triangle \mathrm{ABC})}{\operatorname{ar}(\triangle \mathrm{BDE})}=\left(\frac{\mathrm{BD}+\mathrm{BD}}{\mathrm{BD}}\right)^{2}$

$\frac{\operatorname{ar}(\Delta \mathrm{ABC})}{\operatorname{ar}(\Delta \mathrm{BDE})}=\left(\frac{2 \mathrm{BD}}{\mathrm{BD}}\right)^{2}$

$\frac{\operatorname{ar}(\Delta \mathrm{ABC})}{\operatorname{ar}(\Delta \mathrm{BDE})}=\frac{4}{1}$

Hence the correct answer is $(c)$