Question.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(1) 2 : 1
(2) 1 : 2
(3) 4 : 1
(4) 1 : 4
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(1) 2 : 1
(2) 1 : 2
(3) 4 : 1
(4) 1 : 4
Solution:
$(\because B C=2 B D)$
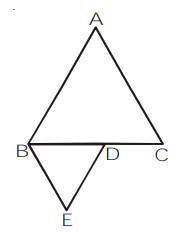
Since, both are equilateral triangles
$\Delta \mathrm{ABC} \sim \Delta \mathrm{EBD}$
$\frac{\operatorname{ar} \Delta \mathrm{ABC}}{\operatorname{ar} \Delta \mathrm{BDE}}=\left(\frac{\mathrm{BC}}{\mathrm{BD}}\right)^{2}=\left(\frac{2}{1}\right)^{2}=4: 1$
$(\because B C=2 B D)$

Since, both are equilateral triangles
$\Delta \mathrm{ABC} \sim \Delta \mathrm{EBD}$
$\frac{\operatorname{ar} \Delta \mathrm{ABC}}{\operatorname{ar} \Delta \mathrm{BDE}}=\left(\frac{\mathrm{BC}}{\mathrm{BD}}\right)^{2}=\left(\frac{2}{1}\right)^{2}=4: 1$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
