ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC.

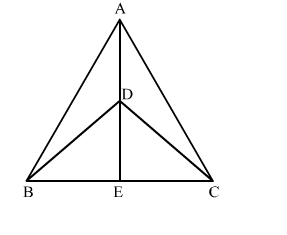
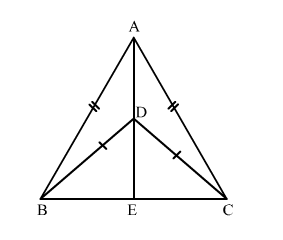
Given: ΔABC and ΔDBC are two isosceles triangles on the same base BC.

To prove:
(i) ΔABD ≅ ΔACD
(ii) ΔABE ≅ ΔACE
(iii) AE bisects ∠A as well as ∠D
(iv) AE is the perpendicular bisector of BC

Proof:
(i) In ΔABD and ΔACD,

BD = CD                                  (Given, ΔDBC is an isosceles triangles)
AB = AC                                   (Given, ΔABC is an isosceles triangles)
AD = AD                                  (Common side)

∴">∴∴ By SSS congruence criteria,
ΔABD ≅ ΔACD

Also, ∠">∠∠BAD = ∠">∠∠CAD         (CPCT)
or, ∠">∠∠BAE = ∠">∠∠CAE     .....(1)

(ii)
In ΔABE and ΔACE,

AB = AC                                   (Given, ΔABC is an isosceles triangles)
∠">∠∠BAE = ∠">∠∠CAE                       [From (i)]
AE = AE                                  (Common side)

∴">∴∴ By SAS congruence criteria,
ΔABE ≅ ΔACE

Also, BE = CE                    (CPCT)    .....(2)
And, ∠">∠∠AEB = ∠">∠∠AEC         (CPCT)   .....(3)

(iii)
In ΔBED and ΔCED,

BD = CD                                  (Given, ΔDBC is an isosceles triangles)
BE = CE                                   [From (2)]
DE = DE                                  (Common side)

∴">∴∴ By SSS congruence criteria,
ΔBED ≅ ΔCED

Also, ∠">∠∠BDE = ∠">∠∠CDE         (CPCT)   .....(4)

(iv)
∵">∵∵ ∠">∠∠BAE = ∠">∠∠CAE        [From (1)]
And, ∠">∠∠BDE = ∠">∠∠CDE   [From (4)]
∴">∴∴ AE bisects ∠A as well as ∠D.

(v)

$\because \angle A E B+\angle A E C=180^{\circ} \quad($ Linear pair $)$

$\Rightarrow \angle A E B+\angle A E B=180^{\circ} \quad[$ From $(3)]$

$\Rightarrow 2 \angle A E B=180^{\circ}$

$\Rightarrow \angle A E B=\frac{180^{\circ}}{2}$

$\Rightarrow \angle A E B=90^{\circ} \quad \ldots .(5)$

From (2) and (5), we get
AE is the perpendicular bisector of BC.