Question:
∆ABC and ∆DBC lie on the same side of BC, as shown in the figure. From a point P on BC, PQ ∥ AB and PR ∥ BD are drawn, meeting AC at Q and CD at R, respectively. Prove that QR ∥ AD.
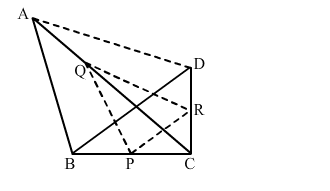
Solution:
In $\triangle C A B, P Q \| A B$.
Applying Thales' theorem, we get:
$\frac{C P}{P B}=\frac{C Q}{Q A} \quad \ldots(1)$
Similarly, applying Thales' theorem in $\triangle B D C$, where $P R \| B D$, we get:
$\frac{C P}{P B}=\frac{C R}{R D} \quad \cdots(2)$
Hence, from $(1)$ and $(2)$, we have :
$\frac{C Q}{Q A}=\frac{C R}{R D}$
Applying the converse of Thales' theorem, we conclude that $Q R \| A D$ in $\triangle A D C$.
This completes the proof.
