ΔABC is a right triangle right angled at A such that AB = AC and bisector of ∠C intersects the side AB at D.

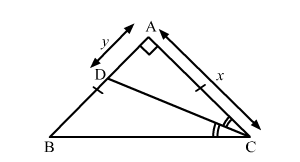
Given: In right triangle ΔABC, ∠BAC = 90°°, AB = AC and ∠ACD = ∠BCD. 

To prove: AC + AD = BC

Proof:
Let AB = AC = x and AD = y.

In Δ∆ABC,

$B C^{2}=A B^{2}+A C^{2}$

$\Rightarrow B C^{2}=x^{2}+x^{2}$

$\Rightarrow B C^{2}=2 x^{2}$

$\Rightarrow B C=\sqrt{2 x^{2}}$

$\Rightarrow B C=x \sqrt{2}$

Now,

$\frac{B D}{A D}=\frac{B C}{A C}$     (An angle bisector of an angle of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle.)

$\Rightarrow \frac{x-y}{y}=\frac{x \sqrt{2}}{x}$

$\Rightarrow \frac{x}{y}-\frac{y}{y}=\sqrt{2}$

$\Rightarrow \frac{x}{y}-1=\sqrt{2}$

$\Rightarrow \frac{x}{y}=(\sqrt{2}+1)$

$\Rightarrow y=\frac{x}{(\sqrt{2}+1)}$

$\Rightarrow y=\frac{x}{(\sqrt{2}+1)} \times \frac{(\sqrt{2}-1)}{(\sqrt{2}-1)}$

$\Rightarrow y=\frac{x(\sqrt{2}-1)}{(\sqrt{2})^{2}-1^{2}}$

$\Rightarrow y=\frac{x \sqrt{2}-x}{2-1}$

$\Rightarrow y=x \sqrt{2}-x$

$\Rightarrow x+y=x \sqrt{2}$

Hence, AC + AD = BC.