Question:
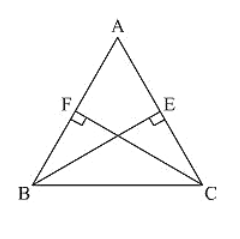
ABC is a triangle in which BE and CF are, respectively, the perpendiculars to the sides AC and AB. If BE = CF, prove that ΔABC is isosceles
Solution:
Given that ABC is a triangle in which BE and CF are perpendicular to the sides AC and AS respectively such that BE = CF.
To prove, ΔABC is isosceles
Now, consider ΔBCF and ΔCBE,
We have
∠BFC = CEB = 90 [Given]
BC = CB [Common side]
And CF = BE [Given]
So, by RHS congruence criterion, we have
ΔBFC ≅ ΔCEB
Now,
∠FBC = ∠EBC [Incongruent triangles corresponding parts are equal]
∠ABC = ∠ACB
AC = AB [Opposite sides to equal angles are equal in a triangle]
ΔABC is isosceles
