ABC is a triangle right angled at C.

Solution:



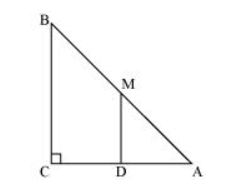
(i) $\ln \triangle \mathrm{ABC}$,

It is given that $M$ is the mid-point of $A B$ and $M D \| B C$.

Therefore, $D$ is the mid-point of $A C$. (Converse of mid-point theorem)

(ii) $A s D M \| C B$ and $A C$ is a transversal line for them, therefore,

$\angle \mathrm{MDC}+\angle \mathrm{DCB}=180^{\circ}$ (Co-interior angles)

$\angle \mathrm{MDC}+90^{\circ}=180^{\circ}$

$\angle \mathrm{MDC}=90^{\circ}$

$\therefore \mathrm{MD} \perp \mathrm{AC}$

(iii) Join $\mathrm{MC}$.



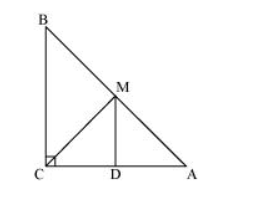
In $\triangle \mathrm{AMD}$ and $\triangle \mathrm{CMD}$,

$\mathrm{AD}=\mathrm{CD}(\mathrm{D}$ is the mid-point of side $\mathrm{AC})$

$\angle A D M=\angle C D M\left(\right.$ Each $\left.90^{\circ}\right)$

DM = DM (Common)

$\therefore \triangle \mathrm{AMD} \cong \triangle \mathrm{CMD}($ By SAS congruence rule $)$

Therefore, $\mathrm{AM}=\mathrm{CM}(\mathrm{By} \mathrm{CPCT})$

However, $A M=\frac{1}{2} A B$ ( $M$ is the mid-point of $A B$ )

Therefore, it can be said that

$\mathrm{CM}=\mathrm{AM}=\frac{1}{2} \mathrm{AB}$