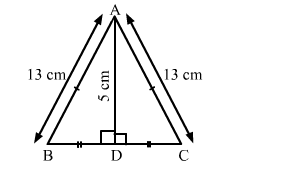
∆ABC is an isosceles triangle with AB = AC = 13 cm.

It is given that $\triangle A B C$ is an isosceles triangle.

Also, AB = AC = 13 cm
Suppose the altitude from A on BC meets BC at D. Therefore, D is the midpoint of BC.
AD = 5 cm

$\triangle A D B$ and $\triangle A D C$ are right-angled triangles.

Applying Pythagoras theorem, we have:

$A B^{2}=A D^{2}+B D^{2}$

$B D^{2}=A B^{2}-A D^{2}=13^{2}-5^{2}$

$B D^{2}=169-25=144$

$B D=\sqrt{144}=12$

Hence,

$B C=2(B D)=2 \times 12=24 \mathrm{~cm}$