Question:
ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
Solution:
Given ABCD is a parallelogram. A circle whose centre O passes through A, B is so drawn that it intersect AD at P and BC at Q To prove Points P, Q, C and D are con-cyclic.
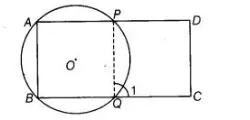
Construction Join PQ
Proof ∠1 = ∠A [exterior angle property of cyclic quadrilateral]
But ∠A = ∠C [opposite angles of a parallelogram]
∴ ∠1 = ∠C ,..(i)
But ∠C+ ∠D = 180° [sum of cointerior angles on same side is 180°]
=> ∠1+ ∠D = 180° [from Eq. (i)]
Thus, the quadrilateral QCDP is cyclic.
So, the points P, Q, C and D are con-cyclic. Hence proved.
