ABCD is a quadrilateral in which AD = BC. If P, Q, R, S

Given:
ABCD is quadrilateral in which AD = BC and P, Q, R, S are the mid points of AB, AC, CD, BD respectively.

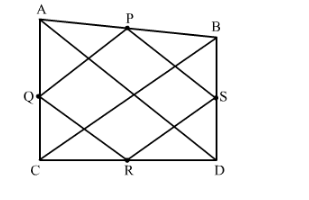
To Prove:
PQRS is  a rhombus.

Proof:
In ∆ABC, P and Q are the midpoints of the sides AB and AC respectively.
By the Mid point theorem, we get
PQ || BC and PQ = 12BC                                                                  ...(1)
In ∆ADC, Q and R are the midpoints of the sides AC and DC respectively.
By the Mid point theorem, we get
QR || AD and QR = 12AD = 12BC           (Since AD = BC)         ...(2)

Similarly, in  ∆BCD, we have
RS || BC and RS = 12BC                                                                  ...(3)
In  ∆BAD, we have
PS || AD and PS = 12AD  = 12BC           (Since AD = BC)          ...(4)
From the equations (1), (2), (3), (4), we get
PQ = QR = RS = RS

Thus, PQRS is a rhombus.