ABCD is a rhombus in which altitude

Let sides of a rhombus be $\quad A B=B C=C D=D A=x$

Now, join DB.

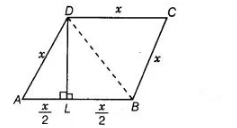
In $\triangle A L D$ and $\triangle B L D, \quad \angle D L A=\angle D L B=90^{\circ}$

[since, $D L$ is a perpendicular bisector of $A B$ ]

$A L=B L=\frac{x}{2}$

and $\quad D L=D L \quad$ [common side]

$\therefore \quad \Delta A L D \cong \triangle B L D \quad$ [by SAS congruence rule]

$A D=B D$ [by CPCT]

Now, in $\triangle A D B$, $A D=A B=D B=x$

Then, $\triangle A D B$ is an equilateral triangle.

$\therefore \quad \angle A=\angle A D B=\angle A B D=60^{\circ}$

Similarly, $\triangle D B C$ is an equilateral triangle.

$\therefore \quad \angle C=\angle B D C=\angle D B C=60^{\circ}$

Also, $\angle A=\angle C$ 

$\therefore \quad \angle D=\angle B=180^{\circ}-60^{\circ}=120^{\circ} \quad$ [since, sum of interior angles is $180^{\circ}$ ]