ABCD is a square. F is the mid-point of AB.

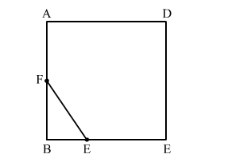
It is given that F is the midpoint of AB. Therefore, we have AF = FB.

It is also given that $B E=\frac{1}{3} B C$...(1)

Now look at the figure. Quadrilateral ABCD is a square and hence all angles are of 90º.

In $\triangle F B E, \angle B=90^{\circ}$ and hence it is a right angle triangle.

We know that the area of the right angle triangle is $\frac{1}{2} \times$ base $\times$ height

Therefore, $A r(\Delta F B E)=\frac{1}{2} \times B F \times B E$

$=108 \mathrm{~cm}^{2}$

Now we will multiple both sides of the equation by 2 we get, $B F \times B E=216$....(2)

But we know that and $B E=\frac{1}{3} B C$.

Let us substitute these values in equation (2) we get,

$\frac{1}{2} \times A B \times \frac{1}{3} \times B C=216$

Let us simplify the above equation as below,

$A B \times B C=6 \times 216$

But we know that ABCD is a square and hence AB = BC = CD = AD.

$\therefore A B^{2}=6 \times 216$...(3)

We know that 216 is the cube of 6 therefore we can write the equation (3) as below,

$\mathrm{AB}^{2}=6^{3} \times 6$

$\mathrm{AB}^{2}=6^{4}$

$\therefore A B=6^{2}=36$

Therefore, side of the square ABCD is 36 cm.

Now we are going to find the diagonal AC.

Diagonal of the square can be calculate by using the formula given below,

Diagonal $=\sqrt{2}$ Side

$A C=\sqrt{2} \times 36$....(4)

We know that $\sqrt{2}=1.414$

Let us substitute the value of $\sqrt{2}$ in equation (3).

$A C=1.414 \times 36$

$=50.904$

Therefore, the length of $\mathrm{AC}$ is $50.904 \mathrm{~cm}$.