Question:
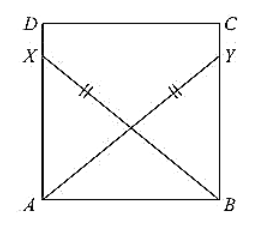
ABCD is a square, X and Y are points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
Solution:
Given that ABCD is a square, X and Y are points on sides AD and BC respectively such that AY = BX.
To prove BY = AX and ∠BAY = ∠ABX
Join B and X, A and Y.
Since, ABCD is a square
∠DAB = ∠CBA = 90°
∠XAB = ∠YAB = 90° .... (i)
Now, consider triangle XAB and YBA
We have
∠XAB = ∠YBA = 90°. [From (i)] BX = AY [given]
And AB = BA [Common side]
So, by RHS congruence criterion, we have ΔXAB ≅ ΔYBA
Now, we know that corresponding parts of congruent triangles are equal.
BY = AX and ∠BAY = ∠ABX
Hence proved
