ABCD is a trapezium in which AB || DC and P,Q

Given, a trapezium ABCD in which AB || DC. P and Q are points on AD and BC, respectively such that PQ || DC. Thus, AB || PQ || DC.

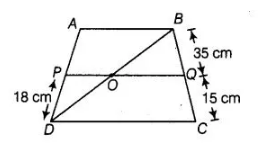
Join BD.

$\ln \triangle A B D$ $P O \| A B$ $[\because P Q \| A B]$

By basic proportionality theorem, $\frac{D P}{A P}=\frac{D O}{O B}$ $\ldots$ (i)

$\ln \Delta B D C$, $O Q \| D C$ $[\because P Q \| D C]$

By basic proportionality theorem,

$\frac{B Q}{Q C}=\frac{O B}{O D}$

$\Rightarrow$ $\frac{Q C}{B Q}=\frac{O D}{O B}$ ....(ii)

From Eqs. (i) and (ii), $\frac{D P}{A P}=\frac{Q C}{B Q}$

$\Rightarrow$ $\frac{18}{A P}=\frac{15}{35}$

$\Rightarrow$ $A P=\frac{18 \times 35}{15}=42$

$\therefore$ $A D=A P+D P=42+18=60 \mathrm{~cm}$