ABCD is a trapezium such that AB and CD

Question:

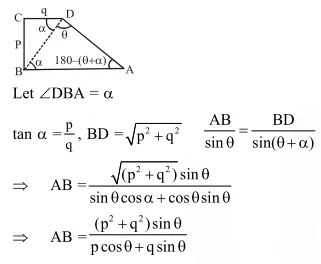
$\mathrm{ABCD}$ is a trapezium such that $\mathrm{AB}$ and $C D$ are parallel and $\mathrm{BC} \perp \mathrm{CD}$. If $\angle \mathrm{ADB}=\theta, \mathrm{BC}$ $=\mathrm{p}$ and $\mathrm{CD}=\mathrm{q}$, then $\mathrm{AB}$ is equal to

  1. $\frac{\left(p^{2}+q^{2}\right) \sin \theta}{p \cos \theta+q \sin \theta}$

  2. $\frac{p^{2}+q^{2} \cos \theta}{p \cos \theta+q \sin \theta}$

  3. $\frac{\mathrm{p}^{2}+\mathrm{q}^{2}}{\mathrm{p}^{2} \cos \theta+\mathrm{q}^{2} \sin \theta}$

  4. $\frac{\left(p^{2}+q^{2}\right) \sin \theta}{(p \cos \theta+q \sin \theta)^{2}}$

Correct Option: 1

Solution:

Leave a comment

eSaral Gurukul

NEET

JEE Main

JEE Advanced

Our Telegram Channel

All Study Material