ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).

Solution:



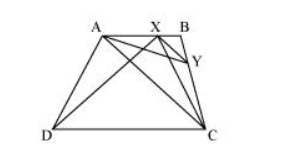
It can be observed that $\triangle \mathrm{ADX}$ and $\triangle \mathrm{ACX}$ lie on the same base $\mathrm{AX}$ and are between the same parallels $\mathrm{AB}$ and $\mathrm{DC}$.

$\therefore$ Area $(\Delta \mathrm{ADX})=$ Area $(\triangle \mathrm{ACX}) \ldots(1)$

$\triangle A C Y$ and $\triangle A C X$ lie on the same base $A C$ and are between the same parallels $A C$ and $X Y$.

$\therefore$ Area $(\triangle \mathrm{ACY})=$ Area $(\mathrm{ACX}) \ldots(2)$

From equations (1) and (2), we obtain

Area $(\triangle \mathrm{ADX})=$ Area $(\triangle \mathrm{ACY})$