AC and BD are chords of a circle which bisect each other. Prove that

Solution:



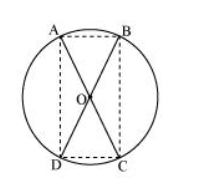
Let two chords AB and CD are intersecting each other at point O.

In $\triangle \mathrm{AOB}$ and $\triangle \mathrm{COD}$,In $\triangle \mathrm{AOB}$ and $\triangle \mathrm{COD}$,

$O A=O C$ (Given)

$O B=O D$ (Given)

$\angle A O B=\angle C O D$ (Vertically opposite angles)

$\triangle \mathrm{AOB} \cong \triangle \mathrm{COD}(\mathrm{SAS}$ congruence rule $)$

$A B=C D(B y C P C T)$

Similarly, it can be proved that $\triangle A O D \cong \triangle C O B$

$\therefore A D=C B(B y C P C T)$

Since in quadrilateral ACBD, opposite sides are equal in length, ACBD is a parallelogram.

We know that opposite angles of a parallelogram are equal.

$\therefore \angle A=\angle C$

However, $\angle \mathrm{A}+\angle \mathrm{C}=180^{\circ}$ (ABCD is a cyclic quadrilateral)

$\Rightarrow \angle \mathrm{A}+\angle \mathrm{A}=180^{\circ}$

$\Rightarrow 2 \angle \mathrm{A}=180^{\circ}$

$\Rightarrow \angle A=90^{\circ}$

As ACBD is a parallelogram and one of its interior angles is 90°, therefore, it is a rectangle.

∠A is the angle subtended by chord BD. And as ∠A = 90°, therefore, BD should be the diameter of the circle. Similarly, AC is the diameter of the circle.