According to Bohr's atomic theory :-
(A) Kinetic energy of electron is $\propto \frac{Z^{2}}{n^{2}}$.
(B) The product of velocity (v) of electron and principal quantum number $(\mathrm{n})$, 'vn' $\propto Z^{2}$
(C) Frequency of revolution of electron in an
orbit is $\propto \frac{Z^{3}}{n^{3}}$.
(D) Coulombic force of attraction on the
electron is $\propto \frac{Z^{3}}{n^{4}}$.
Choose the most appropriate answer from the options given below :
Correct Option: 4,
According to Bohr's theory :
(A) $\mathrm{KE}=13.6 \frac{\mathrm{z}^{2}}{\mathrm{n}^{2}} \frac{\mathrm{eV}}{\text { atom }} \Rightarrow \mathrm{KE} \alpha \frac{\mathrm{z}^{2}}{\mathrm{n}^{2}}$
(B) speed of $\mathrm{e}^{-} \alpha \frac{\mathrm{z}}{\mathrm{n}}$
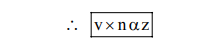
(C) Frequency of revolution of $\mathrm{e}^{-}=\frac{\mathrm{v}}{2 \pi \mathrm{r}}$

(D) $\mathrm{F}=\frac{\mathrm{kq}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}=\frac{\mathrm{kze}^{2}}{\mathrm{r}^{2}} \quad\left\{\mathrm{r} \alpha \frac{\mathrm{n}^{2}}{\mathrm{z}}\right.$
$\Rightarrow \mathrm{F} \alpha \frac{\mathrm{z}}{\left(\frac{\mathrm{n}^{2}}{\mathrm{z}}\right)^{2}}$
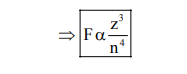
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
