All the vertices of a rhombus lie on a circle.

Let the radius of the circle be r.

Given that. Area of the circle $=1256 \mathrm{~cm}^{2}$

$\pi r^{2}=1256$

$\Rightarrow$  $r^{2}=\frac{1256}{\pi}=\frac{1256}{3.14}=400$

$\Rightarrow$ $r^{2}=(20)^{2}$

$\Rightarrow$ $r=20 \mathrm{~cm}$

$\therefore$ So, the radius of circle is $20 \mathrm{~cm}$. 

$\Rightarrow$ Diameter of circle $=2 \times$ Radius

$=2 \times 20$

$=40 \mathrm{~cm}$

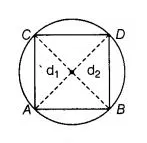
Since, all the vertices of a rhombus lie on a circle that means each diagonal of a rhombus must pass through the centre of a circle that is why both

diagonals are equal and same as the diameter of the given circle.

Let $d_{1}$ and $d_{2}$ be the diagonals of the rhombus.

$\therefore \quad d_{1}=d_{2}=$ Diameter of circle $=40 \mathrm{~cm}$

So, $\quad$ Area of rhombus $=\frac{1}{2} \times d_{1} \times d_{2}$

$=\frac{1}{2} \times 40 \times 40$

$=20 \times 40=800 \mathrm{~cm}^{2}$

Hence, the required  area of rhombus is 800 cm²