An aeroplane leaves an airport and flies due north at a speed of 1000 km/hr. At the same time,

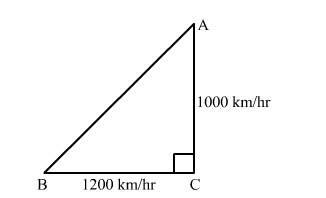
Let A be the first aeroplane flied due north at a speed of 1000 km/hr and B be the second aeroplane flied due west at a speed of 1200 km/hr

Distance covered by plane A in $1 \frac{1}{2}$ hours $=1000 \times \frac{3}{2}=1500 \mathrm{~km}$

Distance covered by plane B in $1 \frac{1}{2}$ hours $=1200 \times \frac{3}{2}=1800 \mathrm{~km}$

Now, In right triangle ABC
By using Pythagoras theorem, we have

$\mathrm{AB}^{2}=\mathrm{BC}^{2}+\mathrm{CA}^{2}$

$=(1800)^{2}+(1500)^{2}$

$=3240000+2250000$

$=5490000$

$\therefore \mathrm{AB}^{2}=5490000$

$\Rightarrow \mathrm{AB}=300 \sqrt{61} \mathrm{~m}$

Hence, the distance between two planes after $1 \frac{1}{2}$ hours is $300 \sqrt{61} \mathrm{~m}$.