Question:
An aeroplane, with its wings spread $10 \mathrm{~m}$, is flying at a speed of $180 \mathrm{~km} / \mathrm{h}$ in a horizontal direction. The total intensity of earth's field at that part is $2.5 \times 10^{-4} \mathrm{~Wb} / \mathrm{m}^{2}$ and the angle of dip is $60^{\circ}$. The emf induced between the tips of the plane wings will be
Correct Option: , 4
Solution:
$\sum=B \perp v \xi$
$\sin 60^{\circ}-\frac{B_{n}}{u}$
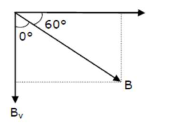
$\frac{\sqrt{3}}{2}=\frac{B_{3}}{B}$
$B V=\frac{\sqrt{3}}{2} B$
$E=\frac{\sqrt{3}}{2} B \ell v$
$=\frac{\sqrt{3}}{2} \times 2.5 \times 10^{-4} \times 10 \times 180 \times \frac{5}{18}$
$=\frac{\sqrt{3}}{2} \times 2.5 \times 5 \times 10^{-2}=10.825 \times 10^{-2}=108.25 \mathrm{mV}$
