Question.
An aircraft is flying at a height of $3400 \mathrm{~m}$ above the ground. If the angle subtended at a ground observation point by the aircraft positions $10.0 \mathrm{~s}$ apart is $30^{\circ}$, what is the speed of the aircraft?
An aircraft is flying at a height of $3400 \mathrm{~m}$ above the ground. If the angle subtended at a ground observation point by the aircraft positions $10.0 \mathrm{~s}$ apart is $30^{\circ}$, what is the speed of the aircraft?
solution:
The positions of the observer and the aircraft are shown in the given figure.
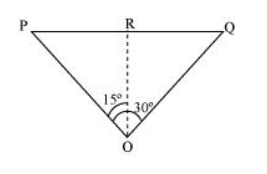
Height of the aircraft from ground, OR = 3400 m
Angle subtended between the positions, $\angle \mathrm{POQ}=30^{\circ}$
Time = 10 s
In $\triangle \mathrm{PRO}:$
$\tan 15^{\circ}=\frac{\mathrm{PR}}{\mathrm{OR}}$
$P R=O R \tan 15^{\circ}$
$=3400 \times \tan 15^{\circ}$
$\triangle \mathrm{PRO}$ is similar to $\triangle \mathrm{RQO}$.
$\therefore P R=R Q$
$P Q=P R+R Q$
$=2 \mathrm{PR}=2 \times 3400 \tan 15^{\circ}$
$=6800 \times 0.268=1822.4 \mathrm{~m}$
$\therefore$ Speed of the aircraft $=\frac{1822.4}{10}=182.24 \mathrm{~m} / \mathrm{s}$
The positions of the observer and the aircraft are shown in the given figure.
Height of the aircraft from ground, OR = 3400 m
Angle subtended between the positions, $\angle \mathrm{POQ}=30^{\circ}$
Time = 10 s
In $\triangle \mathrm{PRO}:$
$\tan 15^{\circ}=\frac{\mathrm{PR}}{\mathrm{OR}}$
$P R=O R \tan 15^{\circ}$
$=3400 \times \tan 15^{\circ}$
$\triangle \mathrm{PRO}$ is similar to $\triangle \mathrm{RQO}$.
$\therefore P R=R Q$
$P Q=P R+R Q$
$=2 \mathrm{PR}=2 \times 3400 \tan 15^{\circ}$
$=6800 \times 0.268=1822.4 \mathrm{~m}$
$\therefore$ Speed of the aircraft $=\frac{1822.4}{10}=182.24 \mathrm{~m} / \mathrm{s}$