An arch is in the form of a parabola with its axis vertical.

The origin of the coordinate plane is taken at the vertex of the arch in such a way that its vertical axis is along the negative y-axis.

This can be diagrammatically represented as

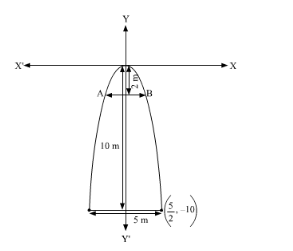
The equation of the parabola is of the form $x^{2}=-4 a y$ (as it is opening downwards).

It can be clearly seen that the parabola passes through point $\left(\frac{5}{2},-10\right)$.

$\left(\frac{5}{2}\right)^{2}=-4 a(-10)$

$\Rightarrow 4 a=\frac{25}{4 \times 10}=\frac{5}{8}$

Therefore, the arch is in the form of a parabola whose equation is $x^{2}=-\frac{5}{8} y$.

When $y=-2, x^{2}=-\frac{5}{8}(-2)$

$\Rightarrow x^{2}=\frac{5}{4}$

$\Rightarrow x=\frac{\sqrt{5}}{2}$

$\therefore \mathrm{AB}=2 \times \frac{\sqrt{5}}{2} \mathrm{~m}=\sqrt{5} \mathrm{~m}=2.23 \mathrm{~m}($ approx. $)$

Hence, when the arch is 2 m from the vertex of the parabola, its width is approximately 2.23 m.