An automobile company uses three types of steel $S_{1}, S_{2}$ and $S_{3}$ for producing three types of cars $C_{1}, C_{2}$ and $C_{3}$. Steel requirements (in tons) for each type of cars are given below
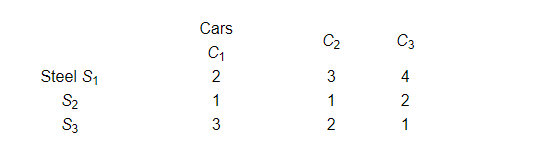
Using Cramer's rule, find the number of cars of each type which can be produced using 29, 13 and 16 tons of steel of three types respectively.
Let $x, y$ and $z$ denote the number of cars that can be produced of each type. Then,
$2 x+3 y+4 z=29$
$x+y+2 z=13$
$3 x+2 y+z=16$
Using Cramer's rule, we get
$D=\left|\begin{array}{lll}2 & 3 & 4 \\ 1 & 1 & 2 \\ 3 & 2 & 1\end{array}\right|$
$=2(1-4)-3(1-6)+4(2-3)$
$=-6+15-4$
$=5$
$D_{1}=\left|\begin{array}{lll}29 & 3 & 4 \\ 13 & 1 & 2 \\ 16 & 2 & 1\end{array}\right|$
$=29(1-4)-3(13-32)+4(26-16)$
$=-87+57+40$
$=10$
$D_{2}=\left|\begin{array}{lll}2 & 29 & 4 \\ 1 & 13 & 2 \\ 3 & 16 & 1\end{array}\right|$
$=2(13-32)-29(1-6)+4(16-39)$
$=-38+145-92$
$=15$
$D_{3}=\left|\begin{array}{lll}2 & 3 & 29 \\ 1 & 1 & 13 \\ 3 & 2 & 16\end{array}\right|$
$=2(16-26)-3(16-39)+29(2-3)$
$=-20+69-29$
$=20$
Thus,
$x=\frac{D_{1}}{D}=\frac{10}{5}=2$
$y=\frac{D_{2}}{D}=\frac{15}{5}=3$
$z=\frac{D_{3}}{D}=\frac{20}{5}=4$
Therefore, $2 C_{1}$ cars, $3 C_{2}$ cars and $4 C_{3}$ cars can be produced using the three types of steel.