An electrician has to repair an electric fault on a pole of height 4 metres. He needs to reach a point 1 metre below the top of the pole to undertake the repair work.

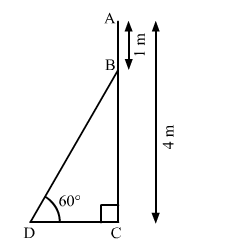
Let AC be the pole and BD be the ladder.

We have,

$\mathrm{AC}=4 \mathrm{~m}, \mathrm{AB}=1 \mathrm{~m}$ and $\angle \mathrm{BDC}=60^{\circ}$

And, $B C=A C-A B=4-1=3 \mathrm{~m}$

In $\Delta \mathrm{BDC}$,

$\sin 60^{\circ}=\frac{\mathrm{BC}}{\mathrm{BD}}$

$\Rightarrow \frac{\sqrt{3}}{2}=\frac{3}{\mathrm{BD}}$

$\Rightarrow \mathrm{BD}=\frac{3 \times 2}{\sqrt{3}}$

$\Rightarrow \mathrm{BD}=2 \sqrt{3}$

$\Rightarrow \mathrm{BD}=2 \times 1.73$

$\therefore \mathrm{BD}=3.46 \mathrm{~m}$

So, he should use 3.46 m long ladder to reach the required position.