Question:
An element crystallises in a face-centred cubic $(f c c)$ unit cell with cell edge $a$. The distance between the centres of two nearest octahedral voids in the crystal lattice is :
Correct Option: 1
Solution:
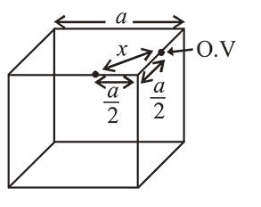
Distance between two octahedral voids
$x=\sqrt{\left(\frac{a}{2}\right)^{2}+\left(\frac{a}{2}\right)^{2}}=\sqrt{\frac{a^{2}}{4}+\frac{a^{2}}{4}}=\frac{a}{\sqrt{2}}$
