An elliptical loop having resistance $R$, of semi major axis $a$, and semi minor axis $b$ is placed in a magnetic field as shown in the figure. If the loop is rotated about the $x$-axis with angular frequency $\omega$, the average power loss in the loop due to Joule heating is :
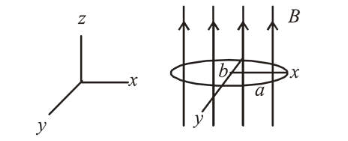
Correct Option: 1
(1) As we know, emf $\varepsilon=N A B \omega \cos \omega t$, Here $N=1$
Average power,
$\langle P\rangle=\left\langle\frac{\varepsilon^{2}}{R}\right\rangle=\left\langle\frac{A^{2} B^{2} \omega^{2} \cos ^{2} \omega t}{R}\right\rangle=\frac{A^{2} B^{2} \omega^{2}}{R}\left(\frac{1}{2}\right)$
Therefore average power loss in the loop due to Joule heating
$
=\frac{\pi^{2} a^{2} b^{2} B^{2}}{2 R}\left(\omega^{2}\right)$
Comments
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.