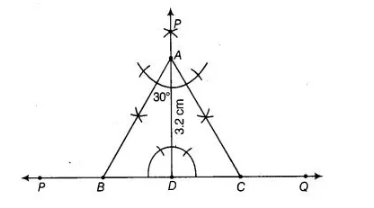
An equilateral triangle,

We know that, in an equilateral triangle all sides are equal and all angles are equal i.e., each angle is of 60°.

Given, altitude of an equilateral triangle say ABC is 3.2 cm. To construct the ΔABC use the following steps.

1. Draw a line PQ.

2. Take a point $D$ on $P Q$ and draw a ray $D E \perp P Q$.

3. Cut the line segment $A D$ of length $3.2 \mathrm{~cm}$ from $D E$.

4. Make angles equal to $30^{\circ}$ at $A$ on both sides of $A D$ say $\angle C A D$ and $\angle B A D$, where $B$ and $C$ lie on $P Q$.

5. Cut the line segment $D C$ from $P Q$ such that $D C=B D$1. Draw a line PQ.

Join AC

Thus, $A A B C$ is the required triangle.

Justification

Here, ∠A = ∠BAD + ∠CAD

= 30°+30° =60°.

Also, AD ⊥ SC

∴ ∠ADS = 90°.

In ΔABD, ∠BAD + ∠DBA = 180° [angle sum property]

30° + 90° + ∠DBA = 180° [∠BAD = 30°, by construction ]

∠DBA = 60°

Similary, ∠DCA = 60°

Thus, ∠A = ∠B=∠C = 60°

Hence, ΔABC is an equilateral triangle.