An incomplete distribution is given below :

Solution:

(i) Let the missing frequencies be x and y.

First we prepare the following cummulative table.

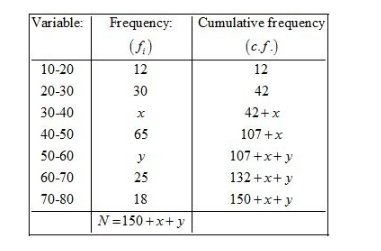
Here, $N=230$

So, $\frac{N}{2}=115$

It is given that the median is 46.

Therefore, $40-50$ is the median class.

$I=40, f=65, F=42+x$ and $h=10$

We know that

Median $=l+\left\{\frac{\frac{N}{2}-F}{f}\right\} \times h$

$46=40+\left\{\frac{115-(42+x)}{65}\right\} \times 10$

$6=\frac{(73-x) \times 10}{65}$

$39=(73-x)$

$x=73-39$

 

$x=34$

Also,

$N=230$

 

$150+x+y=230$

Putting the value of x, we get

$150+34+y=230$

$y=230-184$

$y=46$

Hence, the missing frequencies are 34 and 46.

(ii)

We may prepare the table as shown.

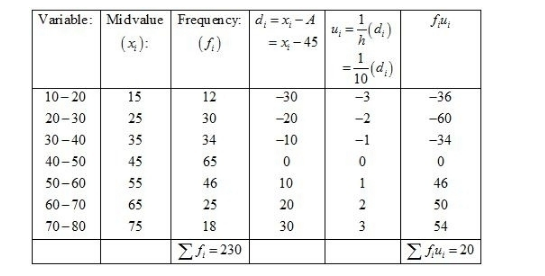
We know that mean, $\bar{X}=A+h\left(\frac{1}{N} \sum f_{i} u_{i}\right)$

Now, we have $N=\sum f_{i}=230, \sum f_{i} u_{i}=20, h=10$ and $A=45$.

Putting the values in the above formula, we have

$\bar{X}=A+h\left(\frac{1}{N} \sum f_{i} u_{i}\right)$

$=45+10\left(\frac{1}{230} \times(20)\right)$

$=45+\frac{200}{230}$

$=45+0.87$

 

$=45.87$

Hence, the mean is 45.87.