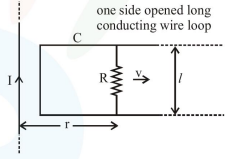
An infinitely long straight wire carrying current I, one side opened rectangular loop and a conductor $\mathrm{C}$ with a sliding connector are located in the same plane, as shown in the figure. The connector has length $l$ and resistance R. It slides to the right with a velocity v. The resistance of the conductor and the self inductance of the loop are negligible. The induced current in the loop, as a function of separation $r$, between the connector and the straight wire is :
Correct Option: 2,
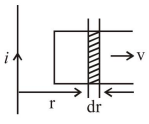
$\mathrm{B}=\frac{\mu_{0} \mathrm{i}}{2 \pi \mathrm{r}}$
$\phi=\frac{\mu_{0} \mathrm{i}}{2 \pi \mathrm{r}} \ell \mathrm{dr}$
$\Rightarrow \frac{\mathrm{d} \phi}{\mathrm{dt}}=\frac{\mu_{0} \mathrm{i} \ell}{2 \pi \mathrm{r}} \cdot \frac{\mathrm{dr}}{\mathrm{dt}}$
$\Rightarrow \mathrm{e}=\frac{\mu_{0}}{2 \pi} \cdot \frac{\mathrm{iv} \ell}{\mathrm{r}}$
$\mathrm{i}=\frac{\mathrm{e}}{\mathrm{R}}=\frac{\mu_{0}}{2 \pi} \cdot \frac{\mathrm{iv} \ell}{\mathrm{Rr}}$
