An object is placed at a distance of $12 \mathrm{~cm}$ from a convex lens. A convex mirror of focal length $15 \mathrm{~cm}$ is placed on other side of lens at $8 \mathrm{~cm}$ as shown in the figure. Image of object coincides with the object.
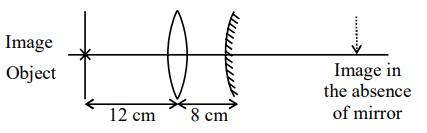
When the convex mirror is removed, a real and inverted image is formed at a position. The distance of the image from the object will be . (cm)
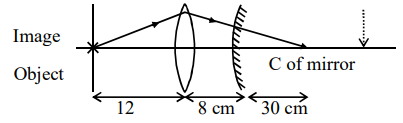
For the object to coincide with image, the light must fall perpendicularly to mirror. Which means that the light will have to converge at $\mathrm{C}$ of mirror. Without the mirror also, the light would coverage at $\mathrm{C}$.
So the distance is : $12+8+30=50 \mathrm{~cm}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
