An observer 1.5 m tall is 20.5 m away from

Let the angle of elevation of the top of the tower from the eve of the observe is $\theta$

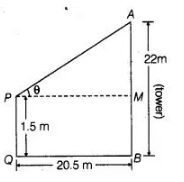
Given that, $\quad A B=22 \mathrm{~m}, P Q=1.5 \mathrm{~m}=M B$

and $\quad Q B=P M=20.5 \mathrm{~m}$

$\Rightarrow \quad A M=A B-M B$

$=22-1.5=20.5 \mathrm{~m}$

Now, in $\triangle A P M, \quad \tan \theta=\frac{A M}{P M}=\frac{20.5}{20.5}=1$

$m \quad \tan A=\tan 45^{\circ}$

$\therefore \quad \theta=45^{\circ}$

which may be either positive or negative.Hence, required angle of elevation of the top of the tower from the eye of the observer is 45°.