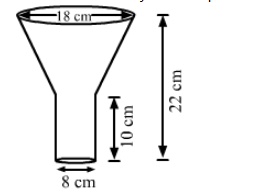
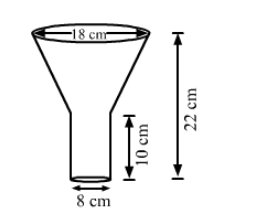
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone.

We have,

Height of the cylindrical portion, $h=10 \mathrm{~cm}$,

Height of the frustum of cone portion, $H=22-10=12 \mathrm{~cm}$,

Radius of the cylindical portion $=$ Radius of smaller end of frustum portion, $r=\frac{8}{2}=4 \mathrm{~cm}$ and

Radius of larger end of frustum portion, $R=\frac{18}{2}=9 \mathrm{~cm}$

Also, the slant height of the frustum, $l=\sqrt{(R-r)^{2}+H^{2}}$

$=\sqrt{(9-4)^{2}+12^{2}}$

$=\sqrt{5^{2}+12^{2}}$

$=\sqrt{25+144}$

$=\sqrt{169}$

$=13 \mathrm{~cm}$

Now,

The area of the tin sheet required $=$ CSA of frustum of cone $+$ CSA of cylinder

$=\pi(R+r) l+2 \pi r h$

$=\frac{22}{7} \times(9+4) \times 13+2 \times \frac{22}{7} \times 4 \times 10$

$=\frac{22}{7} \times 13 \times 13+\frac{22}{7} \times 80$

$=\frac{22}{7} \times(169+80)$

$=\frac{22}{7} \times 249$

$\approx 782.57 \mathrm{~cm}^{2}$

So, the area of the tin sheet required to make the funnel is 782.57 cm2.