An organization selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family.
Question.
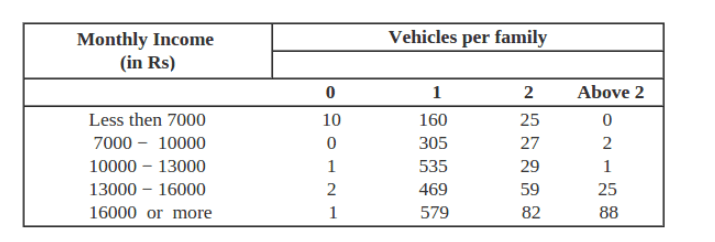
An organization selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below:
Suppose a family is chosen, find the probability that the family chosen is
(i) earning Rs 10000 − 13000 per month and owning exactly 2 vehicles.
(ii) earning Rs 16000 or more per month and owning exactly 1 vehicle.
(iii) earning less than Rs 7000 per month and does not own any vehicle.
(iv) earning Rs 13000 − 16000 per month and owning more than 2 vehicles.
(v) owning not more than 1 vehicle.
An organization selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below:

Suppose a family is chosen, find the probability that the family chosen is
(i) earning Rs 10000 − 13000 per month and owning exactly 2 vehicles.
(ii) earning Rs 16000 or more per month and owning exactly 1 vehicle.
(iii) earning less than Rs 7000 per month and does not own any vehicle.
(iv) earning Rs 13000 − 16000 per month and owning more than 2 vehicles.
(v) owning not more than 1 vehicle.
Solution:
Number of total families surveyed = 10 + 160 + 25 + 0 + 0 + 305 + 27 + 2 + 1 + 535 + 29 + 1 + 2 + 469 + 59 + 25 + 1 + 579 + 82 + 88 = 2400
(i) Number of families earning Rs 10000 − 13000 per month and owning exactly 2 vehicles = 29
Hence, required probability, $\mathrm{P}=\frac{29}{2400}$
(ii) Number of families earning Rs 16000 or more per month and owning exactly 1 vehicle $=579$
Hence, required probability, $P=\frac{579}{2400}$
(iii) Number of families earning less than Rs 7000 per month and does not own any vehicle = 10
Hence, required probability, $\mathrm{P}=\frac{10}{2400}=\frac{1}{240}$
(iv) Number of families earning Rs 13000 − 16000 per month and owning more than 2 vehicles = 25
Hence, required probability, $\mathrm{P}=\frac{25}{2400}=\frac{1}{96}$
(v) Number of families owning not more than 1 vehicle $=10+160+0+305+1+535+2+469+1+579=2062$
Hence, required probability, $\mathrm{P}=\frac{2062}{2400}=\frac{1031}{1200}$
Number of total families surveyed = 10 + 160 + 25 + 0 + 0 + 305 + 27 + 2 + 1 + 535 + 29 + 1 + 2 + 469 + 59 + 25 + 1 + 579 + 82 + 88 = 2400
(i) Number of families earning Rs 10000 − 13000 per month and owning exactly 2 vehicles = 29
Hence, required probability, $\mathrm{P}=\frac{29}{2400}$
(ii) Number of families earning Rs 16000 or more per month and owning exactly 1 vehicle $=579$
Hence, required probability, $P=\frac{579}{2400}$
(iii) Number of families earning less than Rs 7000 per month and does not own any vehicle = 10
Hence, required probability, $\mathrm{P}=\frac{10}{2400}=\frac{1}{240}$
(iv) Number of families earning Rs 13000 − 16000 per month and owning more than 2 vehicles = 25
Hence, required probability, $\mathrm{P}=\frac{25}{2400}=\frac{1}{96}$
(v) Number of families owning not more than 1 vehicle $=10+160+0+305+1+535+2+469+1+579=2062$
Hence, required probability, $\mathrm{P}=\frac{2062}{2400}=\frac{1031}{1200}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
