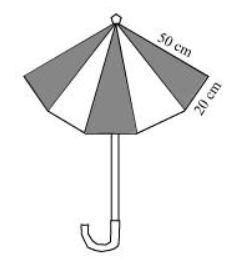
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see the given figure),
Question.
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see the given figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?
Solution:
For each triangular piece,
Semi-perimeter, $s=\frac{(20+50+50) \mathrm{cm}}{2}=60 \mathrm{~cm}$
By Heron's formula,
Area of triangle $=\sqrt{s(s-a)(s-b)(s-c)}$
Area of each triangular piece $=[\sqrt{60(60-50)(60-50)(60-20)}] \mathrm{cm}^{2}$
$=[\sqrt{60(10)(10)(40)}] \mathrm{cm}^{2}=200 \sqrt{6} \mathrm{~cm}^{2}$
Since there are 5 triangular pieces made of two different coloured cloths,
Area of each cloth required $=(5 \times 200 \sqrt{6}) \mathrm{cm}^{2}$
$=1000 \sqrt{6} \mathrm{~cm}^{2}$
For each triangular piece,
Semi-perimeter, $s=\frac{(20+50+50) \mathrm{cm}}{2}=60 \mathrm{~cm}$
By Heron's formula,
Area of triangle $=\sqrt{s(s-a)(s-b)(s-c)}$
Area of each triangular piece $=[\sqrt{60(60-50)(60-50)(60-20)}] \mathrm{cm}^{2}$
$=[\sqrt{60(10)(10)(40)}] \mathrm{cm}^{2}=200 \sqrt{6} \mathrm{~cm}^{2}$
Since there are 5 triangular pieces made of two different coloured cloths,
Area of each cloth required $=(5 \times 200 \sqrt{6}) \mathrm{cm}^{2}$
$=1000 \sqrt{6} \mathrm{~cm}^{2}$