Ankita travels 14 km to her home partly

Let the speed of the rickshaw and the bus are $x$ and $y \mathrm{~km} / \mathrm{h}$, respectively.

Now, she has taken time to travel $2 \mathrm{~km}$ by rickshaw, $t_{1}=\frac{2}{x} \mathrm{~h}$. $\left[\because\right.$ speed $\left.=\frac{\text { distance }}{\text { time }}\right]$

and she has taken time to travel remaining distance $i . e .,(14-2)=12 \mathrm{~km}$ by bus $=t_{2}=\frac{12}{y} \mathrm{~h}$.

By first condition, $t_{1}+t_{2}=\frac{1}{2} \Rightarrow \frac{2}{x}+\frac{12}{y}=\frac{1}{2}$  $\ldots$ (i)

Now, she has taken time to travel $4 \mathrm{~km}$ by rickshaw, $t_{3}=\frac{4}{x} \mathrm{~h}$

and she has taken time to travel remaining distance $i . e .,(14-4)=10 \mathrm{~km}$ by bus $=t_{4}=\frac{10}{y} \mathrm{~h}$.

By second condition, $t_{3}+t_{4}=\frac{1}{2}+\frac{9}{60}=\frac{1}{2}+\frac{3}{20}$

$\Rightarrow \quad \frac{4}{x}+\frac{10}{y}=\frac{13}{20}$ .....(ii)

Let $\frac{1}{x}=u$ and $\frac{1}{y}=v$, then Eqs. (i) and (ii) becomes

$2 u+12 v=\frac{1}{2}$ ....(iii)

and $4 u+10 v=\frac{13}{20}$ ....(iv)

On multiplying in Eq. (iii) by 2 and then subtracting, we get

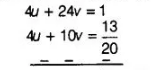
$14 v=1-\frac{13}{20}=\frac{7}{20}$

$\Rightarrow$ $2 v=\frac{1}{20} \Rightarrow v=\frac{1}{40}$

Now, put the value of $v$ in Eq. (iii), we get

$2 u+12\left(\frac{1}{40}\right)=\frac{1}{2}$

$\Rightarrow$ $2 u=\frac{1}{2}-\frac{3}{10}=\frac{5-3}{10}$

$\Rightarrow$ $2 u=\frac{2}{10} \Rightarrow u=\frac{1}{10}$

$\therefore$ $\frac{1}{x}=u$

$\Rightarrow$ $\frac{1}{x}=\frac{1}{10} \Rightarrow x=10 \mathrm{~km} / \mathrm{h}$

and $\frac{1}{y}=v \Rightarrow \frac{1}{y}=\frac{1}{40}$

$\Rightarrow$ $y=40 \mathrm{~km} / \mathrm{h}$

Hence, the speed of rickshaw and the bus are $10 \mathrm{~km} / \mathrm{h}$ and $40 \mathrm{~km} / \mathrm{h}$, respectively.