Question.
(a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere?
(b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?
(c) An artificial satellite orbiting the earth in very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth?
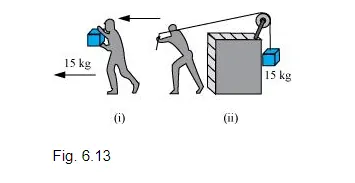
(d) In Fig. 6.13(i) the man walks 2 m carrying a mass of 15 kg on his hands. In Fig. 6.13(ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater?
(a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere?
(b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?
(c) An artificial satellite orbiting the earth in very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth?
(d) In Fig. 6.13(i) the man walks 2 m carrying a mass of 15 kg on his hands. In Fig. 6.13(ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater?

solution:
(a) Rocket
The burning of the casing of a rocket in flight (due to friction) results in the reduction of the mass of the rocket.
According to the conservation of energy:
Total Energy $(T . E .)=$ Potential energy $(P . E .)+$ Kinetic energy $(K . E .)$
$=m g h+\frac{1}{2} m v^{2}$
The reduction in the rocket’s mass causes a drop in the total energy. Therefore, the heat energy required for the burning is obtained from the rocket.
(b) Gravitational force is a conservative force. Since the work done by a conservative force over a closed path is zero, the work done by the gravitational force over every complete orbit of a comet is zero.
(c) When an artificial satellite, orbiting around earth, moves closer to earth, its potential energy decreases because of the reduction in the height. Since the total energy of the system remains constant, the reduction in P.E. results in an increase in K.E. Hence, the velocity of the satellite increases. However, due to atmospheric friction, the total energy of the satellite decreases by a small amount.
(d) In the second case
Case (i)
Mass, m = 15 kg
Displacement, s = 2 m
Work done, $W=F s \cos \theta$
Where, $\theta=$ Angle between force and displacement
$=m g s \cos \theta=15 \times 2 \times 9.8 \cos 90^{\circ}$
$=0$ $\left(\because \cos 90^{\circ}=0\right)$
Case (ii)
Mass, m = 15 kg
Displacement, s = 2 m
Here, the direction of the force applied on the rope and the direction of the displacement of the rope are same.
Therefore, the angle between them, $\theta=0^{\circ}$
Since $\cos 0^{\circ}=1$
Work done, $W=F s \cos \theta=m g s$
$=15 \times 9.8 \times 2=294 \mathrm{~J}$
Hence, more work is done in the second case.
(a) Rocket
The burning of the casing of a rocket in flight (due to friction) results in the reduction of the mass of the rocket.
According to the conservation of energy:
Total Energy $(T . E .)=$ Potential energy $(P . E .)+$ Kinetic energy $(K . E .)$
$=m g h+\frac{1}{2} m v^{2}$
The reduction in the rocket’s mass causes a drop in the total energy. Therefore, the heat energy required for the burning is obtained from the rocket.
(b) Gravitational force is a conservative force. Since the work done by a conservative force over a closed path is zero, the work done by the gravitational force over every complete orbit of a comet is zero.
(c) When an artificial satellite, orbiting around earth, moves closer to earth, its potential energy decreases because of the reduction in the height. Since the total energy of the system remains constant, the reduction in P.E. results in an increase in K.E. Hence, the velocity of the satellite increases. However, due to atmospheric friction, the total energy of the satellite decreases by a small amount.
(d) In the second case
Case (i)
Mass, m = 15 kg
Displacement, s = 2 m
Work done, $W=F s \cos \theta$
Where, $\theta=$ Angle between force and displacement
$=m g s \cos \theta=15 \times 2 \times 9.8 \cos 90^{\circ}$
$=0$ $\left(\because \cos 90^{\circ}=0\right)$
Case (ii)
Mass, m = 15 kg
Displacement, s = 2 m
Here, the direction of the force applied on the rope and the direction of the displacement of the rope are same.
Therefore, the angle between them, $\theta=0^{\circ}$
Since $\cos 0^{\circ}=1$
Work done, $W=F s \cos \theta=m g s$
$=15 \times 9.8 \times 2=294 \mathrm{~J}$
Hence, more work is done in the second case.
