Apply division algorithm to find the quotient

Solution:

(i) We have

$f(x)=x^{3}-6 x^{2}+11 x-6$

$g(x)=x^{2}+x+1$

Here, degree $[f(x)]=3$ and

Degree $(g(x))=2$

Therefore, quotient $q(x)$ is of degree $3-2=1$ and the remainder $r(x)$ is of degree less than 2

Let $q(x)=a x+b$ and

$r(x)=c x+d$

Using division algorithm, we have

$f(x)=g(x) \times q(x)+r(x)$

$x^{3}-6 x^{2}+11 x-6=\left(x^{2}+x+1\right)(a x+b)+c x+d$

$x^{3}-6 x^{2}+11 x-6=a x^{3}+a x^{2}+a x+b x^{2}+b x+b+c x+d$

$x^{3}-6 x^{2}+11 x-6=a x^{3}+a x^{2}+b x^{2}+a x+b x+c x+b+d$

$x^{3}-6 x^{2}+11 x-6=a x^{3}+(a+b) x^{2}+(a+b+c) x+b+d$

Equating the co-efficients of various powers of $x$ on both sides, we get

On equating the co-efficient of $x^{3}$

$x^{3}=a x^{3}$

$x^{x}=a x^{x}$

$1=a$

On equating the co-efficient of $x^{2}$

$-6 x^{2}=(a+b) x^{2}$

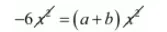
$-6=a+b$

Substituting $a=1$

$-6=1+b$

$-6-1=b$

$-7=b$

On equating the co-efficient of $x$

$11 x=(a+b+c) x$

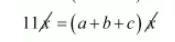
$11=a+b+c$

Substituting $a=1$; and $b=-7$ we get,

$11=1+(-7)+c$

$11=-6+c$

$11+6=c$

$17=c$

On equating the constant terms

$-6=b+d$

Substituting $b=-7$ we get,

$-6=-7+d$

$-6+7=d$

$1=d$

Therefore, 

Quotient $q(x)=a x+b$

$=(1 x-7)$

And remainder $r(x)=c x+d$

$=(17 x+1)$

Hence, the quotient and remainder is given by,

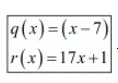
(ii) We have

$f(x)=10 x^{4}+17 x^{3}-62 x^{2}+30 x-3$

$g(x)=2 x^{2}+7 x+1$

Here, Degree $(f(x))=4$ and

Degree $(g(x))=2$

Therefore, quotient $q(x)$ is of degree $4-2=2$ and remainder $r(x)$ is of degree less than 2

$(=\operatorname{deg} \operatorname{ree}(g(x)))$

Let $g(x)=a x^{2}+b x+c$ and

$r(x)=p x+q$

Using division algorithm, we have

$f(x)=g(x) \times q(x)+r(x)$

$10 x^{4}+17 x^{3}-62 x^{2}+30 x-3=\left(2 x^{2}+7 x+1\right)\left(a x^{2}+b x+c\right)+p x+q$

$10 x^{4}+17 x^{3}-62 x^{2}+30 x-3=2 a x^{4}+7 a x^{3}+a x^{2}+2 b x^{3}+7 b x^{2}+b x+2 c x^{2}+7 x c+c+p x+q$

$10 x^{4}+17 x^{3}-62 x^{2}+30 x-3=2 a x^{4}+7 a x^{3}+2 b x^{3}+a x^{2}+7 b x^{2}+2 c x^{2}+b x+7 x c+p x+c+q$

$10 x^{4}+17 x^{3}-62 x^{2}+30 x-3=2 a x^{4}+x^{3}(7 a+2 b)+x^{2}(a+7 b+2 c)+x(b+7 c+p)+c+q$

Equating the co-efficients of various powers $x$ on both sides, we get

On equating the co-efficient of $x^{4}$

$2 a=10$

$a=\frac{10}{2}$

$a=5$

On equating the co-efficient of $x^{3}$

$7 a+2 b=17$

Substituting $a=5$ we get

$7 \times 5+2 b=17$

$35+2 b=17$

$2 b=17-35$

$2 b=-18$

$b=\frac{-18}{2}$

$b=-9$

On equating the co-efficient of $x^{2}$

$a+7 b+2 c=-62$

Substituting $a=5$ and $b=-9$, we get

$5+7 \times-9+2 c=-62$

$5-63+2 c=-62$

$2 c=-62+63-5$

$2 c=-4$

$c=\frac{-4}{2}$

$c=-2$

On equating the co-efficient of $x$

$b+7 c+p=30$

Substituting $b=-9$ and $c=-2$, we get

$-9+7 \times-2+p=30$

$-9-14+p=30$

$-23+p=30$

$p=30+23$

$p=53$

On equating constant term, we get

$c+q=-3$

Substituting $c=-2$, we get

$-2+q=-3$

$q=-3+2$

$q=-1$

Therefore, quotient $q(x)=a x^{2}+b x+c$

$=5 x^{2}-9 x-2$

Remainder $r(x)=p x+q$

$=53 x-1$

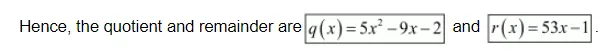
(iii) we have

$f(x)=4 x^{3}+8 x+8 x^{2}+7$

$g(x)=2 x^{2}-x+1$

Here, Degree $(f(x))=3$ and

Degree $(g(x))=2$

Therefore, quotient $q(x)$ is of degree $3-2=1$ and

Degree $(g(x))=2$

Therefore, quotient $q(x)$ is of degree $3-2=1$ and

Remainder $r(x)$ is of degree less than 2

Let $q(x)=a x+b$ and

$r(x)=c x+d$

Using division algorithm, we have

$f(x)=g(x) \times q(x)+r(x)$

$4 x^{3}+8 x^{2}+8 x+7=\left(2 x^{2}-x+1\right)(a x+b)+c x+d$

$4 x^{3}+8 x^{2}+8 x+7=2 a x^{3}-a x^{2}+a x+2 b x^{2}-x b+b+c x+d$

$4 x^{3}+8 x^{2}+8 x+7=2 a x^{3}-a x^{2}+2 b x^{2}+a x-x b+c x+b+d$

$4 x^{3}+8 x^{2}+8 x+7=2 a x^{3}+x^{2}(-a+2 b)+x(a-b+c)+b+d$

Equating the co-efficient of various Powers of $x$ on both sides. we get

On equating the co-efficient of $x^{3}$

$2 a=4$

$a=\frac{4}{2}$

$a=2$

On equating the co-efficient of $x^{2}$

$8=-a+2 b$

Substituting $a=2$ we get

$8=-2+2 b$

Substituting $a=2$ we get

$8=-2+2 b$

$8+2=2 b$

$10=2 b$

$\frac{10}{2}=b$

$5=b$

On equating the co-efficient of $x$

$a-b+c=8$

Substituting $a=2$ and $b=5$ we get

$2-5+c=8$

$-3+c=8$

$c=8+3$

$c=11$

On equating the constant term, we get

$b+d=7$

Substituting $b=5$, we get

$5+d=7$

$d=7-5$

$d=2$

Therefore, quotient $q(x)=a x+b$

$=2 x+5$

Remainder $r(x)=c x+d$

$=11 x+2$

(iv) Given,

$f(x)=15 x^{3}-20 x^{2}+13 x-12$

$g(x)=2-2 x+x^{2}$

Here, Degree $(f(x))=3$ and

Degree $(g(x))=2$

Therefore, quotient $q(x)$ is of degree $3-2=1$ and'

Remainder $r(x)$ is of degree less than 2

Let $q(x)=a x+b$ and

$r(x)=c x+d$

Using division algorithm, we have 

$f(x)=g(x) \times q(x)+r(x)$

$15 x^{3}-20 x^{2}+13 x-12=\left(x^{2}-2 x+2\right)(a x+b)+c x+d$

$15 x^{3}-20 x^{2}+13 x-12=a x^{3}-2 a x^{2}+2 a x+b x^{2}-2 b x+2 b+c x+d$

$15 x^{3}-20 x^{2}+13 x-12=a x^{3}-2 a x^{2}+b x^{2}+2 a x-2 b x+c x+2 b+d$

$15 x^{3}-20 x^{2}+13 x-12=a x^{3}-x^{2}(2 a-b)+x(2 a-2 b+c)+2 b+d$

Equating the co-efficients of various powers of $x$ on both sides, we get

On equating the co-efficient of $x^{3}$

$a x^{3}=15 x^{3}$

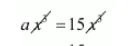
$a=15$

On equating the co-efficient of $x^{2}$

$2 a-b=20$

Substituting $a=15$, we get

$2 \times 15-b=20$

$30-b=20$

$-b=20-30$

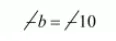
On equating the co-efficient of $x$

$2 a-2 b+c=13$

Substituting $a=15$ and $b=10$, we get

$2 \times 15-2 \times 10+c=13$

$30-20+c=13$

$10+c=13$

$c=13-10$

$c=3$

On equating constant term

$2 b+d=-12$

Substituting $b=10$, we get

$2 \times 10+d=-12$

$20+d=-12$

$d=-12-20$

$d=-32$

Therefore, quotient $q(x)=a x+b$

$=15 x+10$

Remainder $r(x)=3 x-32$

$=3 x-32$