Question:
Area of the largest triangle that can be inscribed in a semi-circle of radius r units is
(a) $r^{2}$ squnits
(b) $\frac{1}{2} r^{2}$ sq units
(c) $2 r^{2}$ sq units
(d) $\sqrt{2} r^{2}$ sq units
Solution:
(a) Take a point $\mathrm{C}$ on the circumference of the semi-circle and join it by the end points of diameter $\mathrm{A}$ and $\mathrm{B}$.
$\therefore \quad \angle C=90^{\circ}$ [by property of circle]
[angle in a semi-circle are right angle]
So, $\triangle A B C$ is right angled triangle.
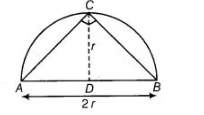
$\therefore$ Area of largest $\triangle A B C=\frac{1}{2} \times A B \times C D$
$=\frac{1}{2} \times 2 r \times r$
$=r^{2}$ sq units
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
