As observed from the top of a 75m high lighthouse from the sea-level,

In the figure, let AB represent the light house.

$\therefore \quad \mathrm{AB}=75 \mathrm{~m}$Let the two ships be C and D such that angle of depression from A are $45^{\circ}$ and $30^{\circ}$ respectively.

Now, in right $\triangle \mathrm{ABC}$, we have

$\frac{\text { AB }}{\text { BC }}=\tan 45^{\circ}$

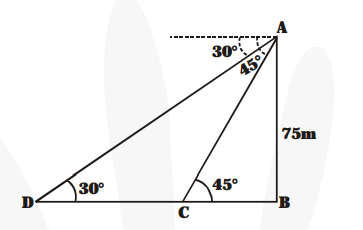
$\Rightarrow \frac{\mathbf{7 5}}{\mathbf{B C}}=1 \Rightarrow \mathrm{BC}=75$

Again, in right $\triangle \mathrm{ABD}$, We have

$\frac{\mathbf{A B}}{\mathbf{B D}}=\tan 30^{\circ} \Rightarrow \frac{\mathbf{7 5}}{\mathbf{B D}}=\frac{\mathbf{1}}{\sqrt{\mathbf{3}}}$

$\Rightarrow \mathrm{BD}=75 \sqrt{\mathbf{3}}$

Since the distance between the two ships

$=\mathrm{CD}=\mathrm{BD}-\mathrm{BC}=75 \sqrt{3}-75=75[\sqrt{3}-1]$

$=75[1.732-1]=75 \times 0.732=54.9$

Thus, the required distance between the ships is $54.9 \mathrm{~m}$.